圆反演变换

定义

给定反演中心点 $O$ 和反演半径 $R$ 。若平面上点 $P$ 和 $P'$ 满足：

• 点 $P'$ 在射线 $\overrightarrow{OP}$ 上
• $|OP| \cdot |OP'| = R^2$

则称点 $P$ 和点 $P'$ 互为反演点。

下图所示即为平面上一点 $P$ 的反演：

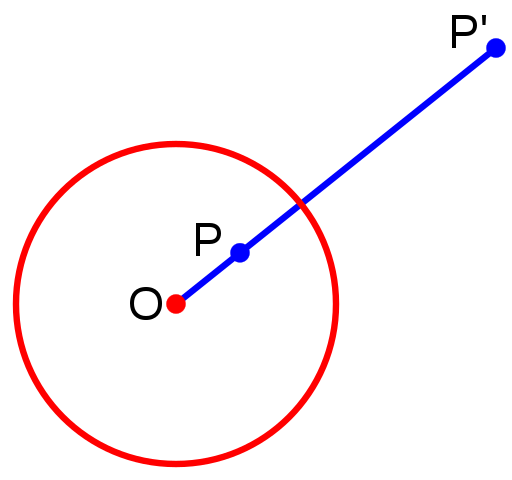
性质

1. 圆 $O$ 外的点的反演点在圆 $O$ 内，反之亦然；圆 $O$ 上的点的反演点为其自身。

2. 不过点 $O$ 的圆 $A$ ，其反演图形也是不过点 $O$ 的圆。

   

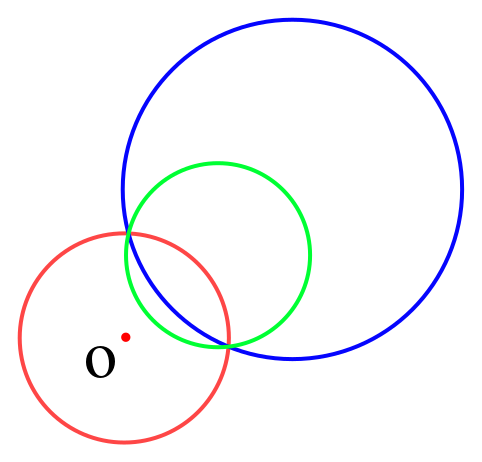
   • 记圆 $A$ 半径为 $r_1$ ，其反演图形圆 $B$ 半径为 $r_2$ ，则有：

     $$r_2 = \frac{1}{2}\left(\frac{1}{|OA| - r_1} - \frac{1}{|OA| + r_1}\right) R^2$$

     证明：

     

     根据反演变换定义：

     $$|OC|\cdot|OC'| = (|OA|+r_1)\cdot(|OB|-r_2) = R^2 \\ |OD|\cdot|OD'| = (|OA|-r_1)\cdot(|OB|+r_2) = R^2$$

     消掉 $|OB|$ ，解方程即可。

   • 记点 $O$ 坐标为 $(x_0, y_0)$ ，点 $A$ 坐标为 $x_1, y_1$ ，点 $B$ 坐标为 $x_2, y_2$ ，则有：

     $$x_2 = x_0 + \frac{|OB|}{|OA|} (x_1 - x_0) \\ y_2 = y_0 + \frac{|OB|}{|OA|} (y_1 - y_0)$$

     其中 $|OB|$ 可在上述求 $r_2$ 的过程中计算得到。

3. 过点 $O$ 的圆 $A$ ，其反演图形是不过点 $O$ 的直线。

   

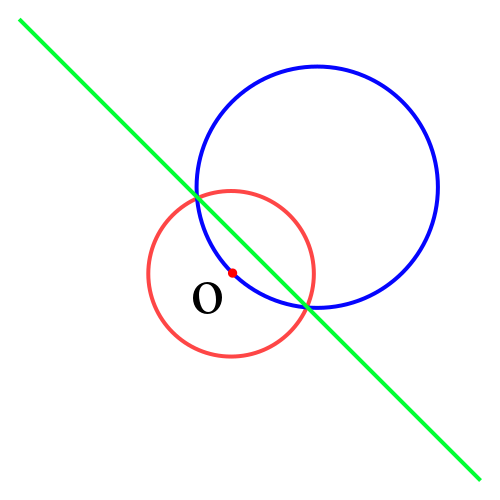
   考虑证明

   

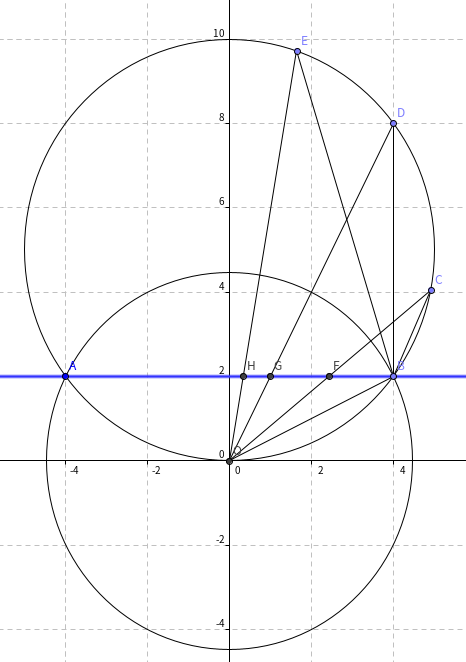
   显然有 \ang E=\ang D=\ang C=\ang OBF=\ang OBG=\ang OBH

   则 $C,D,E$ 的反演点 $F,G,H$ 共线。

4. 两个图形相切，则他们的反演图形也相切。

用途

过反演中心的圆反演为直线，所以遇到给定几个圆，求过某点的圆，与给定圆相交个数的最大值的时候可以考虑反演，然后就可以把问题转换为求切线，在反演回去。

例题

20210224 模拟赛 T1