行列式

定义

对于方阵 $A$ 定义行列式 $|A|$ 或 $det(A)$ 为 $\sum\limits_{p}\left((-1)^{\tau(p)}\prod a_{i,p_i}\right)$ ， $p$ 为排列， $\tau(p)$ 为逆序对个数。

性质

$|A^T|=|A|$

证明：显然 ~~不会证~~
将 $A$ 某一行或某一列乘 $k$ ，则 $|A|$ 变为原来的 $k$ 倍。

证明：改变的这一行中的元素会在每一个 $(-1)^{\tau(p)}\prod a_{i,p_i}$ 中出现一次，提出 $k$ 即可。
令 $A=\begin{bmatrix}X\\z_1\\Y\end{bmatrix},B=\begin{bmatrix}X\\z_2\\Y\end{bmatrix},C=\begin{bmatrix}X\\z_1+z_2\\Y\end{bmatrix}$ （ $X,Y$ 为矩阵， $z_1,z_2$ 为矩阵中的某一行），则 $|A|+|B|=|C|$ 。

证明：

设改变第 $k$ 行。

将 $|C|$ 的定义式展开，考虑某排列 $p$ 对应的一项为

$\begin{aligned} (-1)^{\tau(p)}\prod c_{i,p_i}&=(-1)^{\tau(p)}c_{1,p_1}\cdot c_{2,p_2}\cdots c_{k,p_k}\cdots c_{n,p_n}\\ &=(-1)^{\tau(p)}c_{1,p_1}\cdot c_{2,p_2}\cdots (a_{k,p_k}+b_{k,p_k})\cdots c_{n,p_n}\\ &=(-1)^{\tau(p)}\prod a_{i,p_i}+(-1)^{\tau(p)}\prod b_{i,p_i} \end{aligned}$

$A=\begin{bmatrix}\quad X\quad\\z_1\\Y\\z_2\\Z\end{bmatrix},B=\begin{bmatrix}\quad X\quad\\z_2\\Y\\z_1\\Z\end{bmatrix}$ ，则 $|A|=-|B|$ 。

证明：

首先证明排列相关内容
交换排列相邻两数，排列奇偶性改变。证明：显然
交换排列任意两数，排列奇偶性改变。

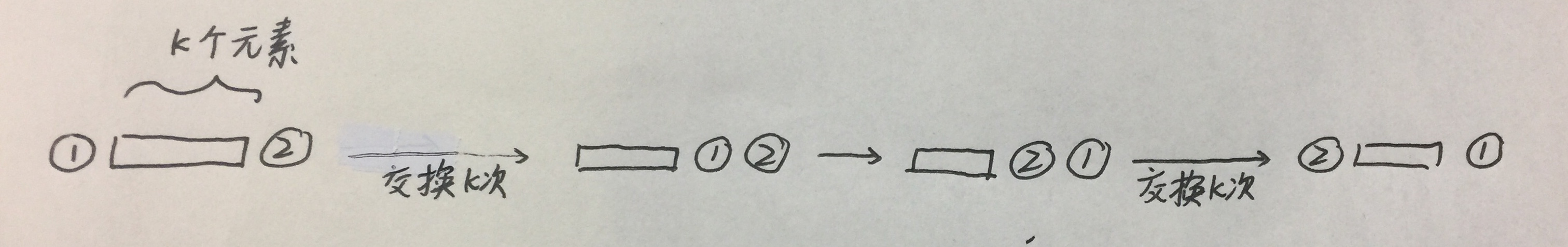
共交换 $2k+1$ 次。

考虑定义式，对于相同的 $a_{i,p_i}$ 每一个排列的奇偶性都改变了，行列式值自然变为原来的相反数。
$A=\begin{bmatrix}\quad X\quad\\z_1\\Y\\kz_1\\Z\end{bmatrix},B=\begin{bmatrix}\quad X\quad\\z_1\\Y\\z_1\\Z\end{bmatrix}$ ，则 $|A|=|B|=0$

证明：首先有 $|A|=k|B|$ ，又有 $B$ 交换两行之后的结果仍为 $B$ ，故 $|B|=-|B|$ ，所以 $|A|=|B|=0$ 。
$A=\begin{bmatrix}\quad X\quad\\z_1\\Y\\z_2\\Z\end{bmatrix},B=\begin{bmatrix}\quad X\quad\\z_1\\Y\\kz_1+z_2\\Z\end{bmatrix}$ ，则 $|A|=|B|$ 。

证明：构造矩阵 $C=\begin{bmatrix}\quad X\quad\\z_1\\Y\\kz_1\\Z\end{bmatrix}$ ，则根据性质 3 有 $|A|+|C|=|B|$ ，而 $|C|=0$ 。

矩阵的逆

定义

定义 $n\times m$ 的矩阵 $A$ 的转置矩阵为 $m\times n$ 的矩阵 $A^T$

定义 $n\times n$ 的方阵 $A$ 的逆为 $A^{-1}$ ，满足 $A\cdot A^{-1}=I$

性质

$(A_1\cdot A_2\cdot\ldots\cdot A_{s})^{T}={A_s}^T\cdot {A_{s-1}}^T\cdot \ldots\cdot {A_1}^T$

证明：不会
$A\cdot A^{-1}=A^{-1}\cdot A$

证明： $A\cdot A^{-1}=A^{-1}\cdot A\cdot A^{-1}\cdot A=A^{-1}\cdot A$
$(A^{-1})^{-1}=A$
$(A^{-1})^T=(A^T)^{-1}$

证明：同时左乘 $A^T$ ，即 $A^T\cdot (A^{-1})^T=A^T\cdot(A^T)^{-1}$
$(A_1\cdots A_s)^{-1}=A_s^{-1}\cdots A_1^{-1}$

证明：同时左乘 $(A_1\cdots A_s)$ 得 $(A_1\cdots A_s)(A_1\cdots A_s)^{-1}=(A_1\cdots A_s)(A_s^{-1}\cdots A_1^{-1})$ 。

等式两边显然等于 $I$ 。

代数余子式和伴随矩阵

定义

对于 $n$ 阶方阵 $A$ ，定义余子式 $M_{i,j}$ 为删去 $a_{i,j}$ 所在的行与列得到的 $n-1$ 阶矩阵。

定义代数余子式 $b_{i,j}=|M_{i,j}|\cdot(-1)^{i+j}$ 。

定义伴随矩阵 $A^*=\begin{bmatrix}b_{1,1}&\cdots&b_{1,n}\\\vdots&\ddots&\vdots\\b_{n,1}&\cdots&b_{n,n}\end{bmatrix}$

性质

$A^{-1}=\cfrac{A^*}{|A|}$ ，其中 $A^*=\begin{bmatrix}b_{1,1}&\cdots&b_{1,n}\\\vdots&\ddots&\vdots\\b_{n,1}&\cdots&b_{n,n}\end{bmatrix}$ 。

证明：知识盲区

推论： $A^{-1}$ 存在 $\Leftrightarrow$ $|A|\neq0$
$AA^*=A^*A=|A|I$

证明：由性质一可以推得
$|A^*|=|A|^{(n-1)}$

证明：在性质二两边取行列式 $|A|\cdot|A^*|=|AA^*|=||A|\cdot I|=|A|^n$ 。
$(A^*)^*=|A|^{(n-2)}\cdot A$

证明：咕咕咕
$|A|=\sum\limits_{j=1}^{n}a_{i,j}b_{i,j}$ （对矩阵 $A$ 第 $i$ 行做 Laplace展开）

求解方法

$O(n^3)$ 的方法：正确的求解代数余子式的方法_Rose_max的博客

初等行变换

初等行变换矩阵

定义

初等行变换矩阵：单位矩阵 $E$ 经过一次初等行变换的结果，三类： $Q_i(v)$ ：将 $e_{i,i}$ 替换成 $v$ ； $R_{i,j}(v)$ ：将第 $j$ 行 $\times v$ 加到第 $i$ 行上； $S_{i,j}$ 交换第 $i$ 和 $j$ 行。

性质

对所有矩阵的初等行变换都可以通过左乘初等行变换矩阵实现。

所有有逆的矩阵都可以表示为 $A=E_1E_2E_3\cdots E_s$ ，其中 $E_i$ 为初等行变换矩阵，则 $A^{-1}={E_k}^{-1}\cdots{E_1}^{-1}$

$\det(Q_i(c)A)=\det(Q_i(c))\det(A)=c\det A$
$\det(R_{i,j}(c)A)=\det R_{i,j}(c)\cdot\det A=\det A$
$\det(S_{i,j}A)=\det S_{i,j}\cdot\det A=\det A$

矩阵的秩

定义

行秩：矩阵的行向量组成的 $n$ 维空间的线性基大小；列秩同理。

性质

矩阵的行秩等于列秩

咕咕