CF708C Centroids
题意简述:
给定一棵 n 个点的树,你可以删除一条边并增加一条边,形成一棵新树。
问每个点在进行这样的操作后,是否可能成为新树的重心。
1≤n≤4⋅105
发现没有是一个无根树,很难处理。考虑把树的重心 rt 找出来,然后想象把这颗树从 rt 处提起来
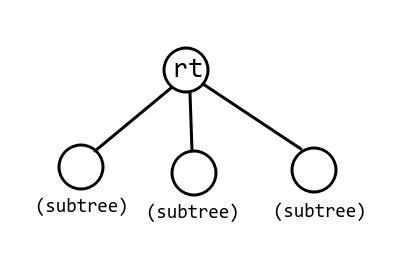
于是对于子树内的每个点 v ,大于 ⌊2n⌋ 的部分只可能出现在 v 的父亲 u 所在联通块上。
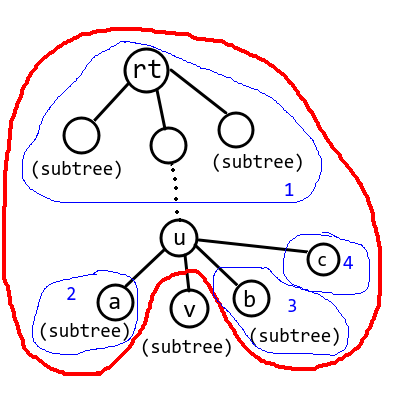
即红色区域。那么我们需要把红色区域拆分成两个大小不大于 ⌊2n⌋ 的部分,分别接到 v 上。
拆分有几个选择,拆掉 u 的父亲所在子树(即上图 1 部分),或者把与 v 同级的子树拆掉,(即上图 2,3,4 )。
设分出来不大于 ⌊2n⌋ 的部分的最大大小为 f(v) ,那么 v 能经过一番操作后变成重心的条件为 n−siz(v)−f(v)≤⌊2n⌋ 。
问题转为求 $ f$ 的值 。
设 v 的父亲为 u,v 的兄弟节点集合为 bro(v)。
设 g(x) 为以 x 为根的子树中,划分出大小不超过 ⌊2n⌋ 的部分的最大大小。
f(v)=max⎩⎪⎪⎪⎨⎪⎪⎪⎧f(u)i∈bro(v)maxg(i)n−siz(v)(n−siz(v)≤⌊2n⌋)
套路: 发现 g(u) 的来源:max{g(v),i∈bro(v)maxg(i)},所以可以优化求 i∈bro(v)maxg(i) 的过程。
设 g(u,0) 表示最大值,g(u,1) 表示次大值,则有:
f(v)=max⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧f(u)g(u,0)g(u,0)=g(v,0)g(u,1)g(u,0)=g(v,0)n−siz(v)(n−siz(v)≤⌊2n⌋)
g 很好求。






