给出 n 个点 Pi(xi,yi),将过这 n 个点的最多 n−1 次(为什么是 n−1 次:因为可以构造出 n 个线性方程,只能解出从常数项系数到 n−1 次项的系数)的多项式记为 f(x) ,求 f(k) 的值。
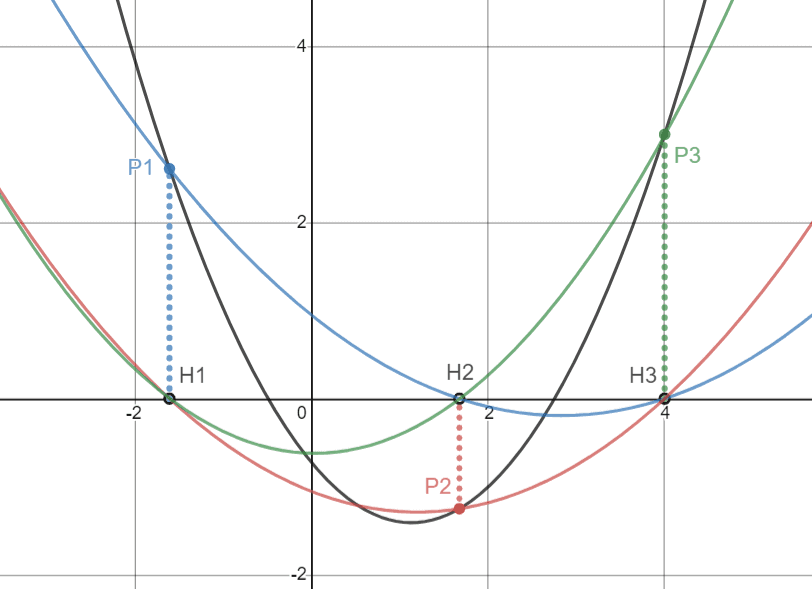
如图所示,将每一个点在 x 轴上的投影 (xi,yi) 记为 Hi 。对每一个 i ,我们选择一个点集 {Pi}∪{Hj∣1≤i≤n,i=j} ,作过这 n 个点的至多 n−1 次的线 gi(x) 。图中 f(x) 用黑线表示,gi(x) 用彩色线表示。
这样得到的 gi(x) 在各自对应的 xi 处取得 yi 的值,在 xj(j=i) 处取得 0。
构造出 gi(x) 表达式:
gi(x)=yij=i∏xi−xjx−xj
代入 xi 可得 gi(x)=yi∏j=ixi−xjxi−xj=yi
代入 xj(j=i) ,gi(x)=yi∏k=ixi−xkxj−xk=yi×0=0
将所有的 gi(x) 求和即可得到 f(x) ,即
f(x)=i=1∑nyij=i∏xi−xjx−xj
求出 f(k)
f(k)=i=1∑nyij=i∏xi−xjk−xj
可以把分子分母都计算出来,再计算一遍逆元,复杂度 O(n2)
文章作者: Cauphenuny
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Cauphenuny's Blog!
相关推荐

2020-10-25
欧拉函数结论
∀n>1\forall n>1∀n>1 ,111 ~ nnn中与 nnn 互质的数的和为 12n×φ(n)\dfrac{1}{2}n\times\varphi(n)21n×φ(n) 证明:gcd(n,x)=gcd(n,n−x)gcd(n,x)=gcd(n,n-x)gcd(n,x)=gcd(n,n−x),所以与 nnn 互质的数成对出现,平均数为 n/2n/2n/2 。 若 p 为素数, φ(pk)=pk(1−1p)=pk−1(p−1)\varphi(p^k)=p^k(1-\dfrac{1}{p})=p^{k-1}(p-1)φ(pk)=pk(1−p1)=pk−1(p−1) φ(n)=n(1−1p1)(1−1p2)…(1−1pk)\varphi(n)=n(1-\dfrac{1}{p_1})(1-\dfrac{1}{p_2})\ldots(1-\dfrac{1}{p_k})φ(n)=n(1−p11)(1−p21)…(1−pk1) 证明:容斥 若 aaa, bbb 互质,则...

2020-10-25
欧拉函数习题
acwing202. 最幸运的数字 P2398 GCD SUM 给定 nnn ,求 ∑i=1n∑j=1ngcd(i,j)\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\gcd(i,j)i=1∑nj=1∑ngcd(i,j) 数据范围:n≤105n\leq10^5n≤105 不需要反演也能做! 挨个枚举 i,ji,ji,j 复杂度太高,考虑枚举 gcd(i,j)\gcd(i,j)gcd(i,j) 的值。 对于所有 gcd(x,y)=1\gcd(x,y)=1gcd(x,y)=1,有 gcd(xk,yk)=k(xk≤n,yk≤n)\gcd(xk,yk)=k\quad(xk\leq n,yk\le n)gcd(xk,yk)=k(xk≤n,yk≤n) 所以 gcd(i,j)=k\gcd(i,j)=kgcd(i,j)=k 的 i,ji,ji,j 的个数为:2∑i=1⌊n/k⌋φ(i)−12\sum\limits_{i=1}^{\lfloor...

2021-02-21
线性代数有关内容
感谢来自 zxyhymzg 的线代小课堂(

2024-01-11
线性代数复习
考前复习

2021-02-18
20210218 模拟赛总结
Index Review 考的不错,主要是第一题做出来了,分数可观, 140pts。 但是后面两题的暴力分也没有打满,这是做的不够的一点。 Solution pk 定义 f(n,k)=(n−k+1)!∑i=0k−1(n−ki)(kj−i−1)f(n,k)=(n-k+1)!\sum_{i=0}^{k-1}\dbinom{n-k}{i}\dbinom{k}{j-i-1}f(n,k)=(n−k+1)!∑i=0k−1(in−k)(j−i−1k) ,求 ∑i=LRf(i+s,i)\sum\limits_{i=L}^{R}f(i+s,i)i=L∑Rf(i+s,i) 经过打表可以发现 f(n,n)=nf(n,n)=nf(n,n)=n 和 f(n,k)=f(n,k+1)⋅kf(n,k)=f(n,k+1)\cdot kf(n,k)=f(n,k+1)⋅k 化简得 f(n,k)=n!(k−1)!f(n,k)=\dfrac{n!}{(k-1)!}f(n,k)=(k−1)!n! type=1 首先考虑 type=1 的情况,代入式子即得...

2021-02-08
FFT 笔记
防止过了几个月就忘了 单位复根 ωn=e2πin=cos(2πn)+i⋅sin(2πn)\omega_n=e^{\frac{2\pi i}{n}}=\cos\left(\dfrac{2\pi}{n}\right)+i\cdot \sin\left(\dfrac{2\pi}{n}\right)ωn=en2πi=cos(n2π)+i⋅sin(n2π) 性质 ωnn=1ωnk=ω2n2kω2nk+n=−ω2nk\begin{aligned} \omega_n^n&=1\\ \omega_n^k&=\omega_{2n}^{2k}\\ \omega_{2n}^{k+n}&=-\omega_{2n}^k\\ \end{aligned} ωnnωnkω2nk+n=1=ω2n2k=−ω2nk 位逆序置换: R(x)=⌊R(⌊x2⌋)2⌋+(x mod 2)×len2R(x)=\left\lfloor \frac{R\left(\left\lfloor \frac{x}{2} \right\rfloor\right)}{2}...
评论