先看一个题目 CF161D Distance in Tree
考虑 dp(当然点分治也可以做),先求出 f(u,k) 表示将树中的 u 作为根节点后,深度为 k 的节点数量,则答案为 2∑u∈Gf(u,k)。
可以暴力求 f 数组,复杂度 O(n2k)。
优化一下,先以 1 为根节点,求出从每个点 u 开始,向下走 k 的路径条数 g(u,k)
设节点 u 的一个儿子是 v 。观察到如果求出了 f(u,k) 那么求 f(v,k) 可以利用一下信息。
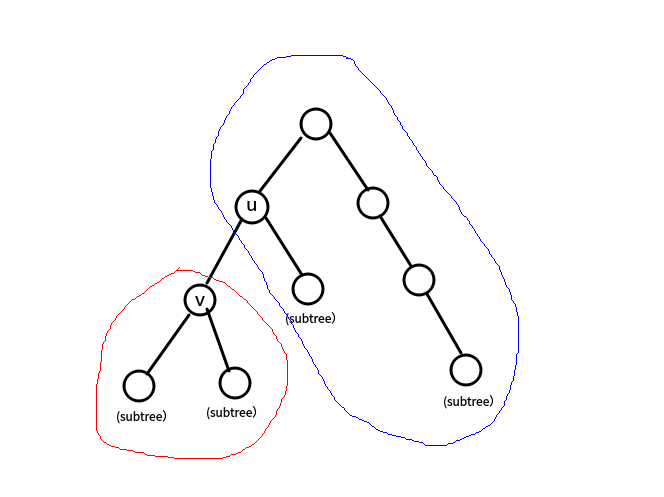
红色部分显然是 g(v,k) ,蓝色部分是 f(u,k−1),但是这样有一部分会多计算,就是那些以 u 为端点,长度为 k−1 ,经过了红色部分的路径。减去 g(v,k−2) 即可。
f(v,k)=g(v,k)+f(u,k−1)−g(v,k−2)
复杂度 O(nk)
文章作者: Cauphenuny
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Cauphenuny's Blog!
相关推荐

2021-01-16
20200116~17 考试总结
这两天考了学长出的一套省选模拟题。(似乎是 Matthew99 /se Day 1 A 建出 SAM 后就是在 parent tree 上找 LCA。 B 是 CF708c 的加强版。 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151//author: ycp | https://ycpedef.github.io//#pragma GCC...

2021-01-09
20210109~10 考试总结
都是雅礼2017集训的题 Day1 T1 决斗 有结论:存在至少一个位置 kkk 满足对于任意的顺序都满足没有精灵从第 kkk 个精灵旁走到第 k+1k+1k+1 个精灵旁。 证明:定义 RiR_iRi 为一开始分配的侏儒对手编号小于或等于 iii 的精灵个数,并定义 Pi=Ri−iP_i =R_i-iPi=Ri−i。Pn=0P_n =0Pn=0 永远成立。不妨设位置 mmm 满足 PmP_mPm 是所有 PiP_iPi 里面最小的,可以证明永远不会有精灵从位置 mmm 走到位置 m+1m+1m+1。假设存在一个精灵从位置 mmm 走到位置 m+1m+1m+1,意味着存在一个序列 a,a+1,a+2,...,m−1,ma, a+1,a+2,...,m-1,ma,a+1,a+2,...,m−1,m 满足初始侏儒对手在这个区间的精灵数大于这些位置的数量。而初始侏儒对手在这个区间的精灵数减去这些位置的数量的差等于 Pm−PaP_m -P_aPm−Pa 。而由于 PmP_ mPm 是所有 PiP_iPi 中最小的,所有 Pm−Pa>0P_m -P_a...

2021-02-18
20210218 模拟赛总结
Index Review 考的不错,主要是第一题做出来了,分数可观, 140pts。 但是后面两题的暴力分也没有打满,这是做的不够的一点。 Solution pk 定义 f(n,k)=(n−k+1)!∑i=0k−1(n−ki)(kj−i−1)f(n,k)=(n-k+1)!\sum_{i=0}^{k-1}\dbinom{n-k}{i}\dbinom{k}{j-i-1}f(n,k)=(n−k+1)!∑i=0k−1(in−k)(j−i−1k) ,求 ∑i=LRf(i+s,i)\sum\limits_{i=L}^{R}f(i+s,i)i=L∑Rf(i+s,i) 经过打表可以发现 f(n,n)=nf(n,n)=nf(n,n)=n 和 f(n,k)=f(n,k+1)⋅kf(n,k)=f(n,k+1)\cdot kf(n,k)=f(n,k+1)⋅k 化简得 f(n,k)=n!(k−1)!f(n,k)=\dfrac{n!}{(k-1)!}f(n,k)=(k−1)!n! type=1 首先考虑 type=1 的情况,代入式子即得...

2021-02-20
20210220 考试总结
Review 考试时一直在肝论文,发现 2017 国集论文里面有决策单调性优化 dp 的内容,终于在考试最后 2 分钟调过样例。 结果因为没有滚数组导致 MLE,沦为暴力 20pts。 Solution T1 hike nnn 个点, qqq 个询问 两种询问,分别是合并两树和查询树中里给定点最远的点的距离 LCT 维护树的直径板子题 O(nlogn)O(n\log n)O(nlogn),可惜我不会,只好启发式合并暴力处理倍增数组。 考虑两颗树的直径端点 a,b,c,da,b,c,da,b,c,d ,则合并出的新树直径只有可能是这 4 个数中的 2...

2021-02-06
CF372C Watching Fireworks is Fun
CF372C Watching Fireworks is Fun 单调队列优化区间 dp 设 f(i,j)f(i,j)f(i,j) 表示放到第 iii 个烟花,当前在 jjj 的位置,设可以在两次烟花之间的移动距离为 sss 可以发现 f(i,j)=minj−s≤k≤j+s(f(i,k))+bi−∣ai−j∣f(i,j)=\min\limits_{j-s\le k\le j +s}(f(i,k))+b_i-\vert a_i-j\vert f(i,j)=j−s≤k≤j+smin(f(i,k))+bi−∣ai−j∣ 用单调队列维护,加滚动数组,时间复杂度 O(nm)O(nm)O(nm) ,空间复杂度 O(n)O(n)O(n)

2020-12-03
CF708C Centroids 总结
CF708C Centroids 题意简述: 给定一棵 nnn 个点的树,你可以删除一条边并增加一条边,形成一棵新树。 问每个点在进行这样的操作后,是否可能成为新树的重心。 1≤n≤4⋅1051 \le n \le 4\cdot 10^51≤n≤4⋅105 发现没有是一个无根树,很难处理。考虑把树的重心 rt 找出来,然后想象把这颗树从 rt 处提起来 于是对于子树内的每个点 v ,大于 ⌊n2⌋\left\lfloor\dfrac{n}{2}\right\rfloor⌊2n⌋ 的部分只可能出现在 v 的父亲 u 所在联通块上。 即红色区域。那么我们需要把红色区域拆分成两个大小不大于 ⌊n2⌋\left\lfloor\dfrac{n}{2}\right\rfloor⌊2n⌋ 的部分,分别接到 v 上。 拆分有几个选择,拆掉 u 的父亲所在子树(即上图 1 部分),或者把与 v 同级的子树拆掉,(即上图 2,3,4 )。 设分出来不大于 ⌊n2⌋\left\lfloor\dfrac{n}{2}\right\rfloor⌊2n⌋ 的部分的最大大小为...
评论